Matemática: Progressão aritmética

Progressão Aritmética (abreviadamente, P. A.) é uma sequência numérica em que cada termo, a partir do segundo, é igual à soma do termo anterior com uma constante $r$ . O número $r$ é chamado de razão ou diferença comum da progressão aritmética.

Alguns exemplos de progressões aritméticas:

1, 4, 7, 10, 13, ..., é uma progressão aritmética em que a razão (a diferença entre os números consecutivos) é igual a 3.
-2, -4, -6, -8, -10, ..., é uma P.A. em que $r = -2$ .
6, 6, 6, 6, 6, ..., é uma P.A. com $r = 0$ .

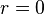Numa progressão aritmética, a partir do segundo termo, o termo central é a média aritmética do termo antecessor e do sucessor, isto é, $a_{n} = (a_{n-1} + a_{n+1}) / 2$ .

Fórmula do termo geral de uma progressão aritmética

O n-ésimo termo de uma progressão aritmética, denotado por $a_n$ , pode ser obtido por meio da formula

$a_n = a_1 + (n - 1) \cdot r,$

em que:

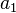$a_1$ é o primeiro termo;
$r$ é a razão.

Por meio da formula acima também é possível inserir (ou interpolar) uma quantidade de meios aritméticos entre dois números dados, de modo que eles formem parte de uma progressão aritmética.Esse procedimento é chamado de interpolação aritmética.

Demonstração

A fórmula do termo geral pode ser demonstrada por indução matemática:

Ela é válida para o segundo termo pois, por definição, cada termo é igual ao anterior mais uma constante fixa r e portanto $a_2 = a_1 + 1 \cdot r;$
Assumindo como hipótese de indução que a fórmula é válida para $n-1$ , ou seja, que $a_{n-1} = a_1 + (n - 2) \cdot r$ , resulta que o n-ésimo termo é dado por:

$a_n = a_{n-1} + r = (a_1 + (n - 2) \cdot r) + r = a_1 + ((n - 2) \cdot r + r) = a_1 + (n - 1) \cdot r.$

De forma análoga, demonstra-se a seguinte fórmula, que expressa o n-ésimo termo em função do m-ésimo termo, para quaisquer inteiros positivos m e n:

$a_n = a_m + (n - m) \cdot r$

Soma dos termos de uma progressão aritmética

A soma dos termos de uma progressão aritmética situados no intervalo fechado de $a_p$ até $a_q$ é calculada pela seguinte fórmula:

$S_{(p,q)}=\frac{(q - p + 1) \cdot (a_p + a_q)}{2}.$

Em particular, para somar os n primeiros termos, pode-se utilizar a seguinte simplificação da fórmula anterior:

$S_n=\frac{n \left(\cdot a_1 + a_n\right)}{2}.$

Diz a lenda que Gauss fora punido pelo professor (por estar desatento numa de suas aulas do ciclo primário de matemática) com a tarefa de somar todos os números inteiros de 1 a 100. Apercebeu-se desta fórmula e utilizou-a para calcular imediatamente a soma pedida. Ao apresentar sua resposta, o professor disse ser impossível o garoto ter realizado a tarefa em tão pouco tempo e duvidou da resposta de Gauss. O garoto só foi levado a sério no final da aula, quando os outros alunos obtiveram a resposta. Dizem também que Gauss chegou a ser punido fisicamente por questionar o professor.

Tipos de progressões aritméticas

Progressão aritmética constante

Uma progressão aritmética constante ou estacionária é toda progressão aritmética em que todos os termos são iguais, sendo que para isso a razão r tem que ser sempre igual a zero.

Exemplos de progressões aritméticas constantes:

5, 5, 5, 5, 5, ..., tem razão r = 0
0, 0, 0, 0, 0, ..., tem razão r = 0

Progressão aritmética crescente

Uma progressão aritmética crescente é toda progressão aritmética em que cada termo, a partir do segundo, é maior que o termo que o antecede, sendo que para isso a razão r tem que ser sempre maior que zero (r>0).

Exemplos de progressões aritméticas crescentes:

2, 4, 6, 8, 10, ..., com razão r = 2
3, 6, 9, 12, 15, ..., com razão r = 3

Progressão aritmética decrescente

Uma progressão aritmética decrescente é toda progressão aritmética em que cada termo, a partir do segundo, é menor que o termo que o antecede, sendo que para isso a razão r tem que ser sempre menor do que zero (r<0).

Exemplos de progressões aritméticas decrescentes:

6, 4, 2, 0, -2, ..., tem razão igual a -2
6, 3, 0, -3, -6, ..., tem razão igual a -3

Progressão aritmética de segunda ordem

Uma progressão aritmética de segunda ordem é uma sequência de números em que as diferenças entre os termos consecutivos segue uma progressão aritmética. Por exemplo, na sequência

1, 3, 7, 13, 21, 31, 43, 57, 73, ...,

se subtrairmos o primeiro termo da sequência do segundo, teremos como resultado o número 2. Já a diferença entre o segundo e terceiro termos é igual a 4, a diferença entre o terceiro e o quarto termos é igual a 6, e assim sucessivamente. Verificamos que a diferença entre os termos da sequência cresce em progressão aritmética de razão igual a 2, ou seja, assume os valores 2, 4, 6, 8 e assim por diante.

Seguindo o mesmo raciocínio, podemos definir progressões aritméticas de ordem 3: são sequências numéricas cuja diferença entre os termos formam uma progressão aritmética de ordem 2. Por analogia, podemos definir progressões aritméticas de ordem n.

O estudo da soma dos termos dessas sequências serve como introdução ao cálculo de integrais de funções polinomiais.

Exemplos:

1) Sabendo que o primeiro termo de uma PA é 5 e a razão é 11, calcule o 13^o termo:

- Primeiro devemos coletar todas informações do problema:
a₁=5 r=11 a₁₃=?
- Para calcular vamos utilizar a fórmula do termo geral, onde a_n será o a₁₃, portanto n=13. Agora, substituindo:

        a₁₃ = 5 + (13 - 1).11
        a₁₃ = 5 + (12).11
        a₁₃ = 5 + 132
        a₁₃ = 137

2) Dados a₅ = 100 e r = 10, calcule o primeiro termo:

        a₅ = a₁ + (5 - 1).r
        100 = a₁ + (5 - 1).10
        100 = a₁ + 40
        100 - 40 = a₁
        a₁ = 60

4) (UFRGS) Em uma Progressão Aritmética, em que o primeiro termo é 23 e a razão é -6, a posição ocupada pelo elemento -13 é:

- informações do problema:
a₁ = 23 r = -6 a_n = -13 n=?

        - Substituindo na fórmula do termo geral:
        a_n = a₁ + (n-1)r
        -13 = 23 + (n - 1).(-6)
        -13 - 23 = -6n + 6
        -36 - 6 = -6n
        -42 = -6n      Vamos multiplicar os dois lados por (-1)
        6n = 42
        n = 42/6
        n = 7