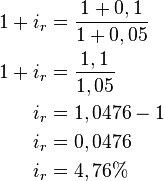Dizemos que uma sequência numérica constitui uma progressão geométrica quando, a partir do 2º termo, o quociente entre um elemento e seu antecessor for sempre igual. Observe a sequência:
(2, 4, 8, 16, 32, 64,...), dizemos que ela é uma progressão geométrica, pois se encaixa na definição dada.
4 : 2 = 2
8 : 4 = 2
16 : 8 = 2
32 : 16 = 2
64 : 32 = 2
O termo constante da progressão geométrica é denominado razão.
Muitas situações envolvendo sequências são consideradas PG, dessa forma, foi elaborada uma expressão capaz de determinar qualquer elemento de uma progressão geométrica. Veja:
(2, 4, 8, 16, 32, 64,...), dizemos que ela é uma progressão geométrica, pois se encaixa na definição dada.
4 : 2 = 2
8 : 4 = 2
16 : 8 = 2
32 : 16 = 2
64 : 32 = 2
O termo constante da progressão geométrica é denominado razão.
Muitas situações envolvendo sequências são consideradas PG, dessa forma, foi elaborada uma expressão capaz de determinar qualquer elemento de uma progressão geométrica. Veja:
.jpg)
Com base nessa expressão, temos que:
a2 = a1 * q
a3 = a1 * q2
a5 = a1 * q4
a10 = a1 * q9
a50 = a1*q49
a100 = a1*q99
Exemplo 1
Em uma progressão geométrica, temos que o 1º termo equivale a 4 e a razão igual a 3. Determine o 8º termo dessa PG.
a8 = 4 * 37
a8 = 4 * 2187
a8 = 8748
O 8º termo da PG descrita é o número 8748.
Exemplo 2
Dada a PG (3, 9, 27, 81, ...), determine o 20º termo.
a20 = 3 * 319
a20 = 3 * 1.162.261.467
a20 = 3.486.784.401
Soma dos termos de uma PG
A soma dos termos de uma PG é calculada através da seguinte expressão matemática:
.jpg)
Exemplo 3
Considerando os dados do exemplo 2, determine a soma dos 20 primeiros elementos dessa PG.

Exemplo 4
Uma dona de casa registrou os gastos mensais com supermercado durante todo o ano. Os valores foram os seguintes:
Janeiro: 98,00
Fevereiro: 99,96
Março: 101,96
Abril: 104,00
Maio: 106,08
Calcule o gasto anual dessa dona de casa, considerando que em todos os meses o índice inflacionário foi constante.
Os termos estão em progressão geométrica, observe:
106,08 : 104 = 1,02
104 : 101,96 = 1,02
101,96 : 99,96 = 1,02
99,96 : 98,00 = 1,02
A razão dessa progressão geométrica é dada por 1,02, isto indica que a inflação entre os meses é de 2%. Vamos determinar a soma dos gastos dessa dona de casa, observe:
.jpg)
Os gastos da dona de casa com compras de supermercado, foram equivalentes a
R$ 1.314,39.













.jpg)
.jpg)
.jpg)
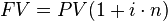
 Valor Futuro (do inglês Future Value)
Valor Futuro (do inglês Future Value)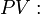 Valor Presente (do inglês Present Value)
Valor Presente (do inglês Present Value) Taxa de juros (do inglês Interest Rate)
Taxa de juros (do inglês Interest Rate) Número de períodos
Número de períodos ) para pagar em 2 meses (
) para pagar em 2 meses ( ) com taxa de juros de 10% ao mês (
) com taxa de juros de 10% ao mês ( ), calculados conforme o regime de juros simples. Depois de 2 meses essa pessoa irá pagar $120, conforme a fórmula:
), calculados conforme o regime de juros simples. Depois de 2 meses essa pessoa irá pagar $120, conforme a fórmula:
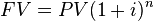

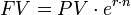
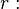 Taxa de juros continuamente composta
Taxa de juros continuamente composta
 , que é continuamente composta, possui significado diferente do valor da taxa de juros
, que é continuamente composta, possui significado diferente do valor da taxa de juros 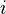 , usada na primeira fórmula. Porém, como ambas são usadas no regime de juros compostos, existe uma fórmula para fazer a "tradução" de uma taxa para outra:
, usada na primeira fórmula. Porém, como ambas são usadas no regime de juros compostos, existe uma fórmula para fazer a "tradução" de uma taxa para outra:

 ). Depois de 2 meses essa pessoa irá pagar $122,14, conforme a fórmula:
). Depois de 2 meses essa pessoa irá pagar $122,14, conforme a fórmula:
 ), o regime de juros simples apresenta valores superiores ao regime de juros compostos.
), o regime de juros simples apresenta valores superiores ao regime de juros compostos.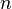

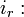 Taxa de juros real
Taxa de juros real Taxa de juros nominal
Taxa de juros nominal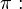 Taxa de inflação
Taxa de inflação ), e durante o mesmo período o índice de preços cresce 5% - ou seja, a inflação é de 5% (
), e durante o mesmo período o índice de preços cresce 5% - ou seja, a inflação é de 5% ( ). A taxa de juros real nesse caso é de 4,76%, conforme a fórmula:
). A taxa de juros real nesse caso é de 4,76%, conforme a fórmula: